发表于 | 分类于 |

Perceptron

How powerful is a perception？（Expressiveness（and，or，not，xor））

  1. and

  1. or

  2. not

represent anything：可以表达由and，or，not组合成的任意逻辑表达式

e.g. XOR

结论：

  1. 感知机是线性的
  2. perceptron can represent anything：可以表达由and，or，not组合成的任意逻辑表达式

Learning

  1. perceptron rule：how to set a single unit

trick：添加W(0)，并设为1，用来表示 threshold value
是否线性可分：如果线性可分，该算法最终为经过有限次迭代后停止

  1. Non-linear separability：Gradient descent
    为什么前面有1/2：求导时，便于消去

  2. 比较
    唯一的区别：是否阈值化

Note：

  1. 梯度下降不直接用y’的原因是，阈值化后，函数不连续

  2. 引出可以使用safter threshold 的连续函数——sigmoid function

  3. sigmoid

Note：这个函数不是唯一的，只是其中的一种，可以近似阈值待定问题的连续函数

Neural Network

Note：

  • whole thing is differentiable：
    • 对于任何一个中间节点，在给定值得情况下，我们知道稍微增加或减少该节点值对输出有什么影响
    • 我们可以调整所有权值，进而使输出与预期更加一致
  • 使用别的连续函数代替sigmoid函数，该模型仍成立
  • Backpropagation：误差的反向传播
  • 与perceptron不同，如果问题线性可分，最终会停下来，得到最优解；梯度下降存在很多局部最优解

advanced optimize methods

Note:

  • complexity
    • Decision Tree：树的深度
    • Regression：多项式的阶数
    • Neural Network
      • #nodes
      • #layers
      • 参数的权重

        Bias

        Restriction bias：representational power——set of hypothesis we will consider

能表示任意函数：

  • 代表着可以表达任何问题，包括训练集中包含的所有噪音
  • 很容易发生overfiting
    • 在给定节点个数和层数的情况下，hypothesis set 的大小是有限
    • cross validation能帮助我们确定节点个数，层数，权重大小

Note：在固定节点个数，层数，权重大小的情况下，随着迭代次数的增加，测试集误差会增加，这反映了神经网络的模型复杂度不仅仅由这三个因素所决定（这是与其他算法不同的地方）

Preference bias：

Conclusion

发表于 | 分类于 |

Representation

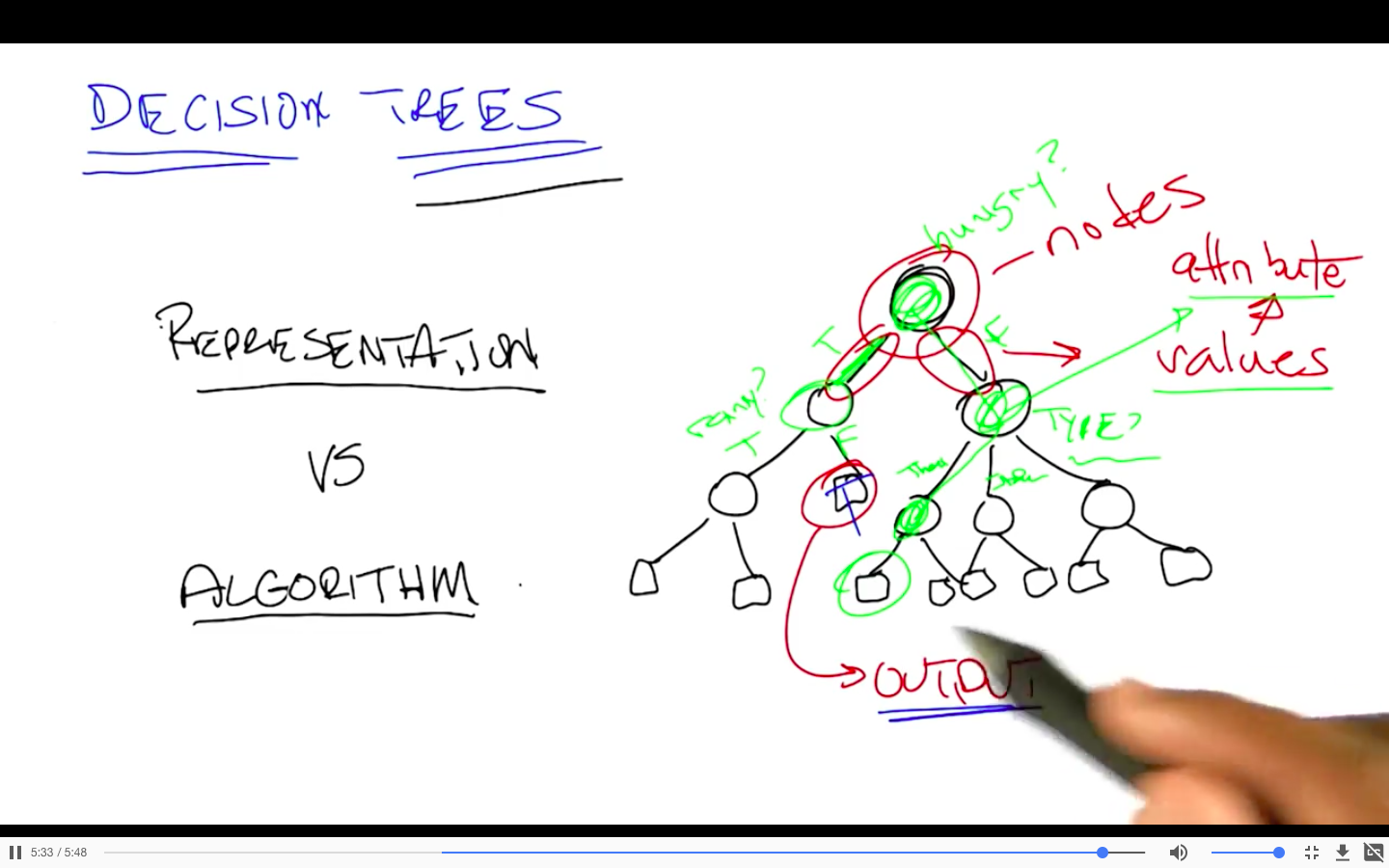
Learning

Expressiveness（and，or，xor）

size of hypothesis set


结论：

  • hypothesis space is very expressive because there’s lots of different functions that you can represent
  • should have some clever way to search among them

Learning Algorithm


熵（直观认识）：measure of information，randomness

P(A) = 1 ：no information，no randomness，no entropy(entropy = 0)

均匀划分时：它们的熵会是最大的

在此不进行展开，将在randomize optimization 中详细介绍

e.g.


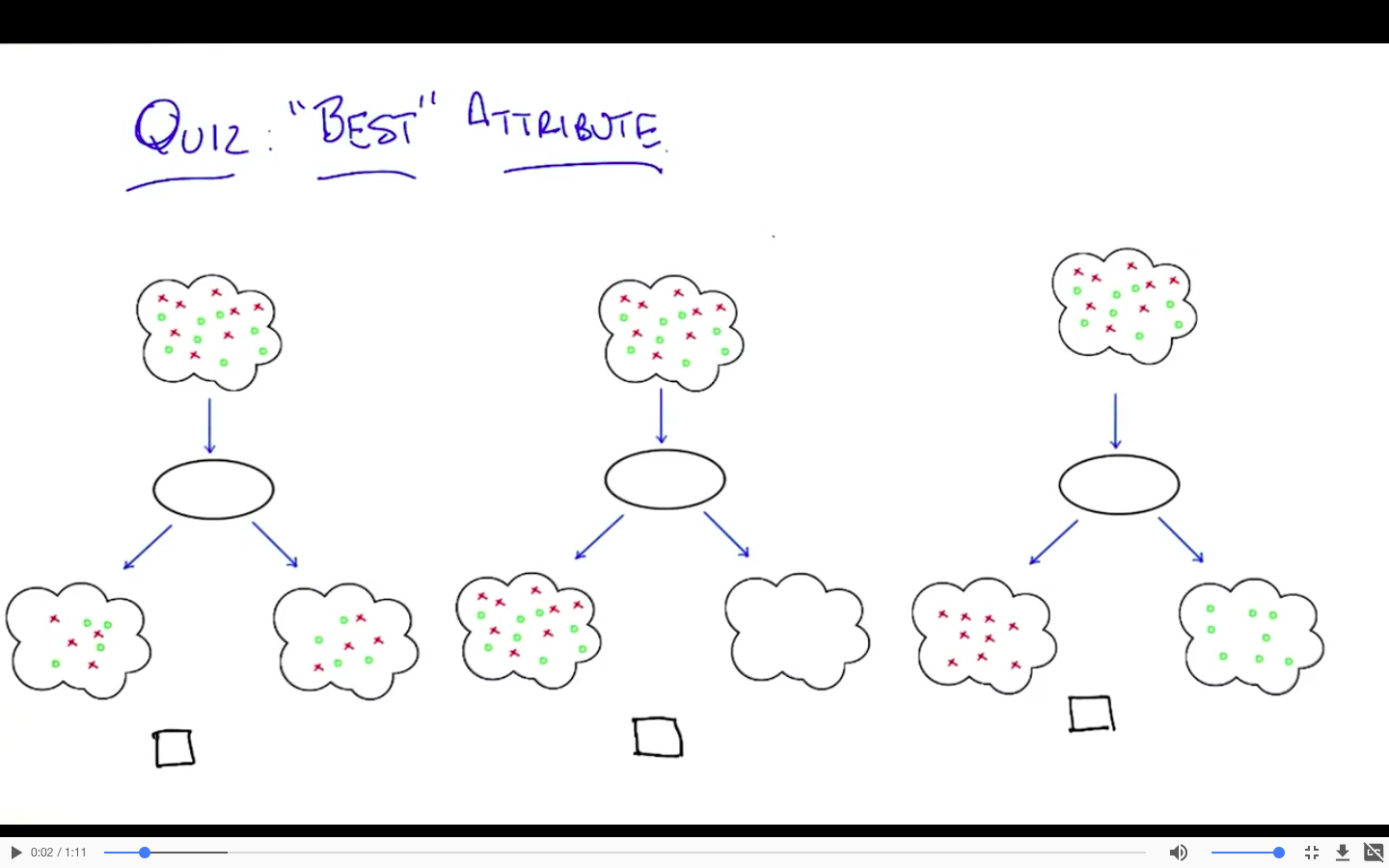
图一图二的entropy没有改变

图三中俩个子集的entropy都减小了，在该例子中，减为0
相应的，它的信息熵的增量是最大的

bias

hypothesis set： all possible decision tree

two kind of biases

  • Restriction bias：H
  • Preference bias：
    • what source of hypothesis from this hypothesis set we prefer

Other considerations

对于存在的噪音该如何处理？

overfitting

  • pruning


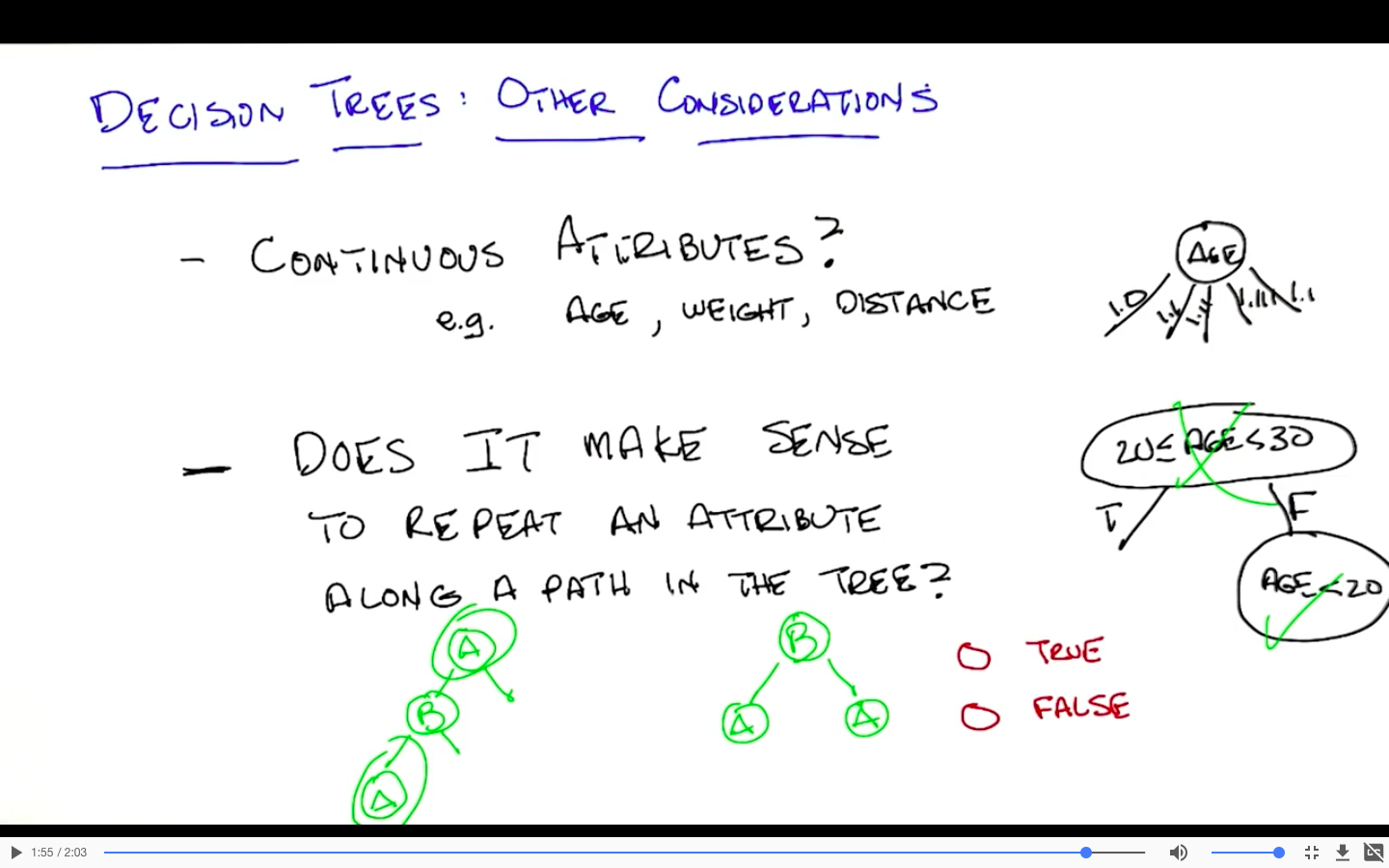
对离散型特征：没有意义
对连续型特征：

  • 不同的问题（范围）：有意义

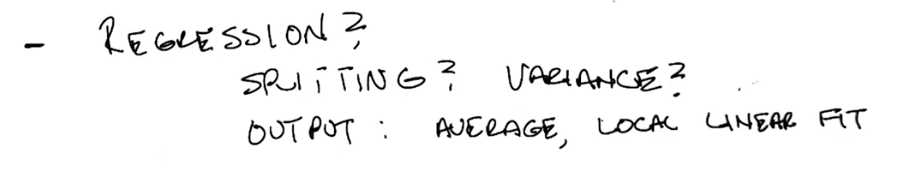
Conclusion

发表于 | 分类于 |

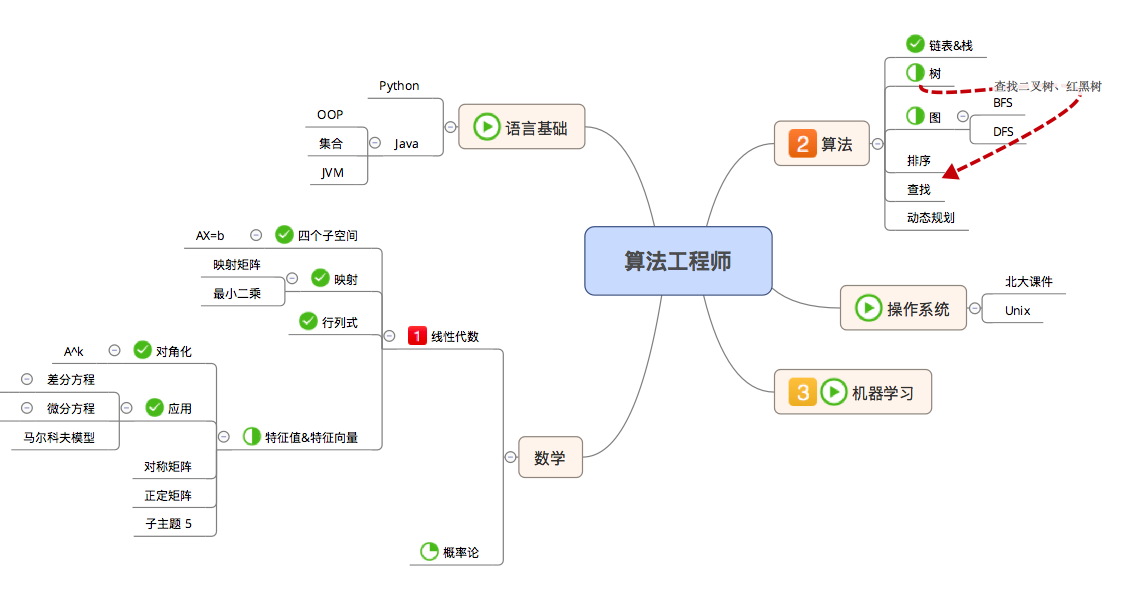
5.2

  • 线性代数
    • 微分方程
    • 马尔科夫矩阵
  • 算法
    • 图论——搜索
      5.3
  • 线性代数
    • 正定矩阵
    • 相似矩阵
      5.4
  • 线性代数
    • SVD
  • 算法实现
    • 割点
    • 并查集
    • BFS
  • 算法
    • 杨氏矩阵
      • 插入
      • 查找
    • 进程调度
      5.5
  • 机器学习
    • Decision Tree
    • Neural Network
  • 博客整理：2篇

5.7

  • 机器学习
    • 回归，邹博
      5.8
  • 机器学习
    • Logistic Regression，邹博
      5.9
  • 机器学习
    • 决策树
      5.10
  • 机器学习
    • 提升，邹博
    • Deep Learning-week2

发表于 | 分类于 |

周一

  • 线性代数
    • 克莱姆法则、逆矩阵、体积[MIT线代第二十课]
    • 特征值和特征向量[MIT线代第二十一课]
    • 对角化和 矩阵A 的幂[MIT线代第二十二课]
  • 练习
    • 线性代数第一次作业

      周二

  • 线性代数
    • 常微分方程，幂【MIT线性代数第二十三课】
  • 算法
    • 树

      周三

  • 线性代数
    • 对称矩阵
  • 概率论

发表于 |