决策树

模型表示

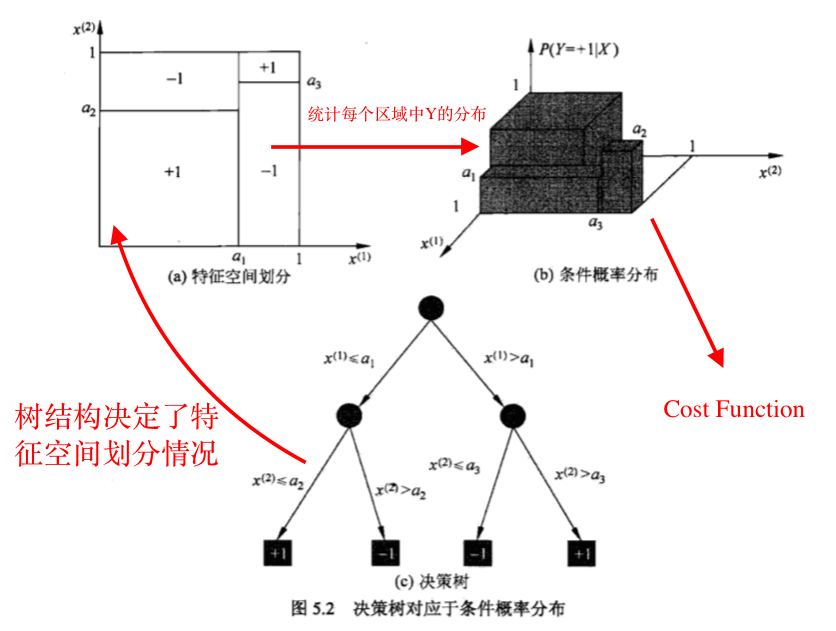
决策树算法的本质是求出最优的特征空间的划分，在这个划分基础上的条件概率P(Y|X)的分布最优

因此还需完成俩步：

1. 定义 cost function
2. 根据cost function怎么构建决策树（因为决策树的结构决定了cost function）

代价函数

从模型表示可以直观地看出，叶子节点中Y的种类越少越好，意味着分错的数量越少

叶子的熵可以量化这一情况

决策树的构建

因此决策树学习的算法转变为了递归选择最优特征的一个过程

接下来给出如何选择，定义最优特征

特征的选择

根据不同的最优特征定义，分别有着不同的决策树学习算法

信息增益

1. 确定度量量
   学习算法的目标就是降低整棵树的信息熵，因此认为最优的特征A是，在确定A后，特征空间D的信息熵减少最多的那个特征
   

2. 条件熵的公式推导
   由此可知，条件熵恰好可以用来帮助选择特征，下面给出条件熵的公式推导，便于计算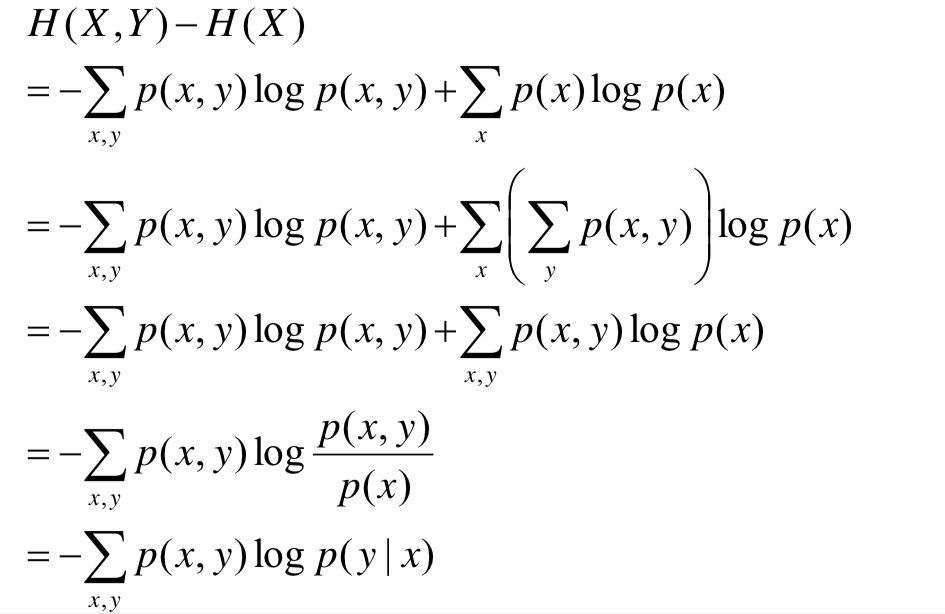
   
   

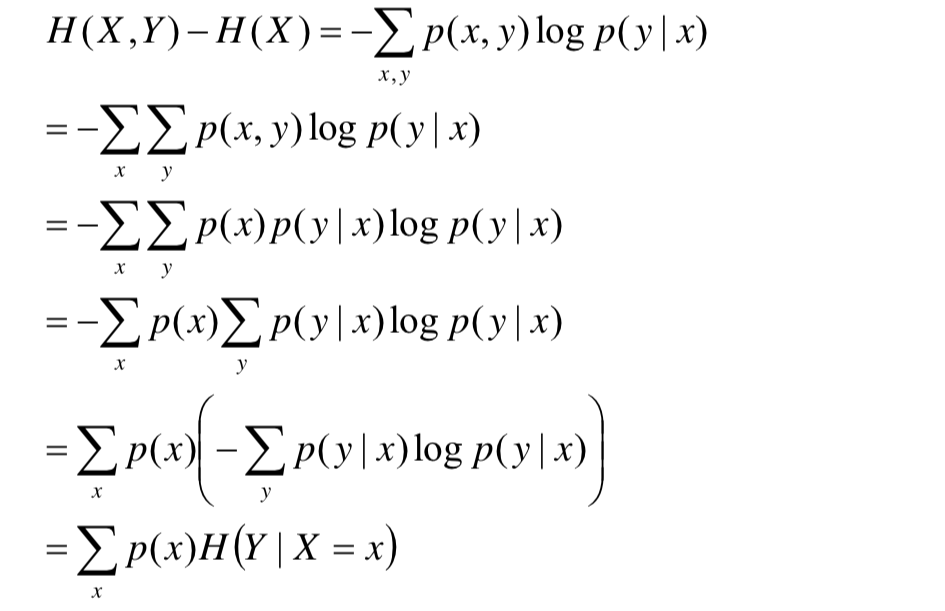
3. 信息增益的定义
   

4. 信息增益的计算
   符号定义
   
   公式计算
   

信息增益比

参考：

1. 邹博博士课件
2. 《统计学习方法》——李航