Representation
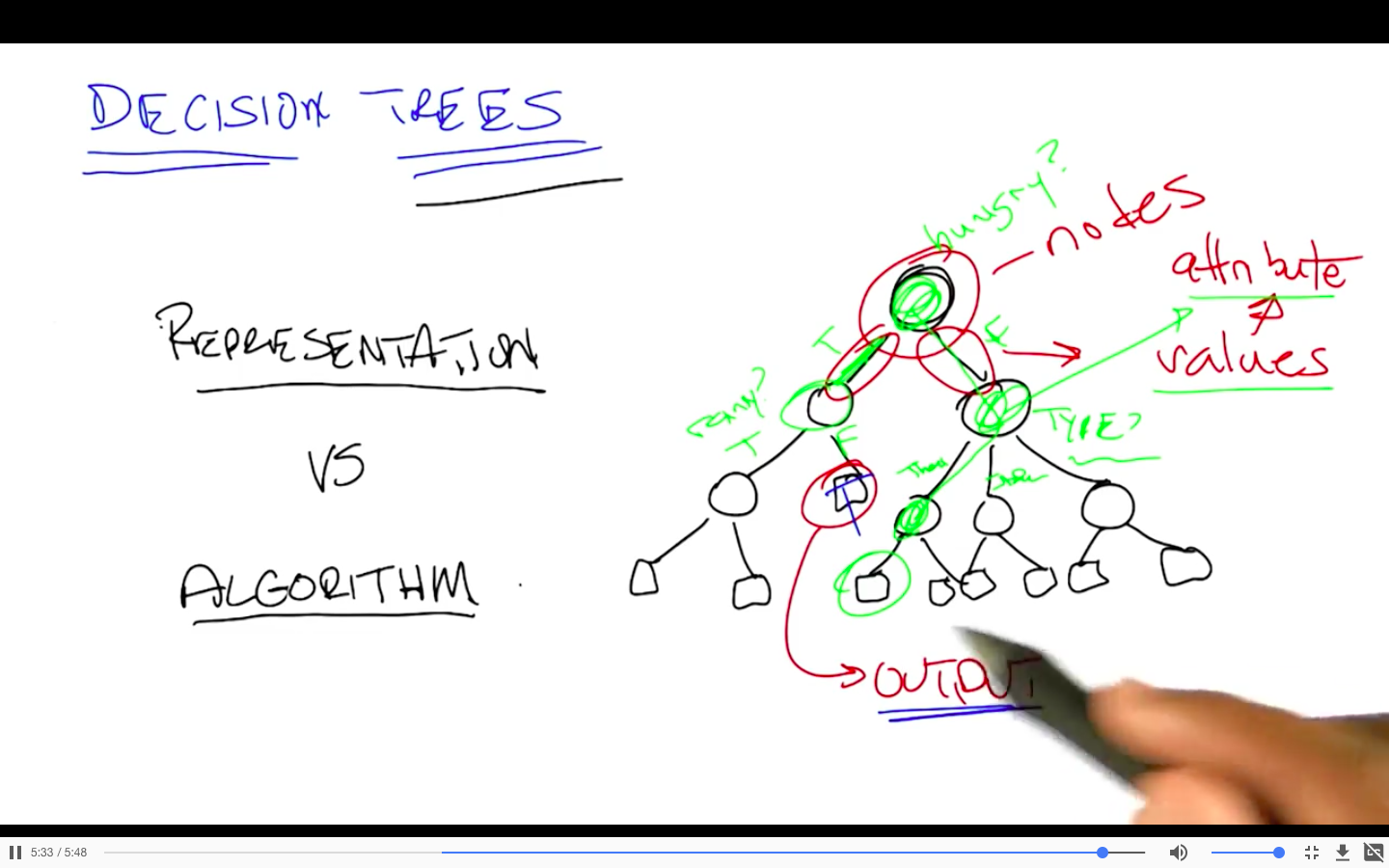
Learning

Expressiveness(and,or,xor)

size of hypothesis set

结论:
- hypothesis space is very expressive because there’s lots of different functions that you can represent
- should have some clever way to search among them
Learning Algorithm

熵(直观认识):measure of information,randomness
P(A) = 1 :no information,no randomness,no entropy(entropy = 0)
均匀划分时:它们的熵会是最大的
在此不进行展开,将在randomize optimization 中详细介绍
e.g.
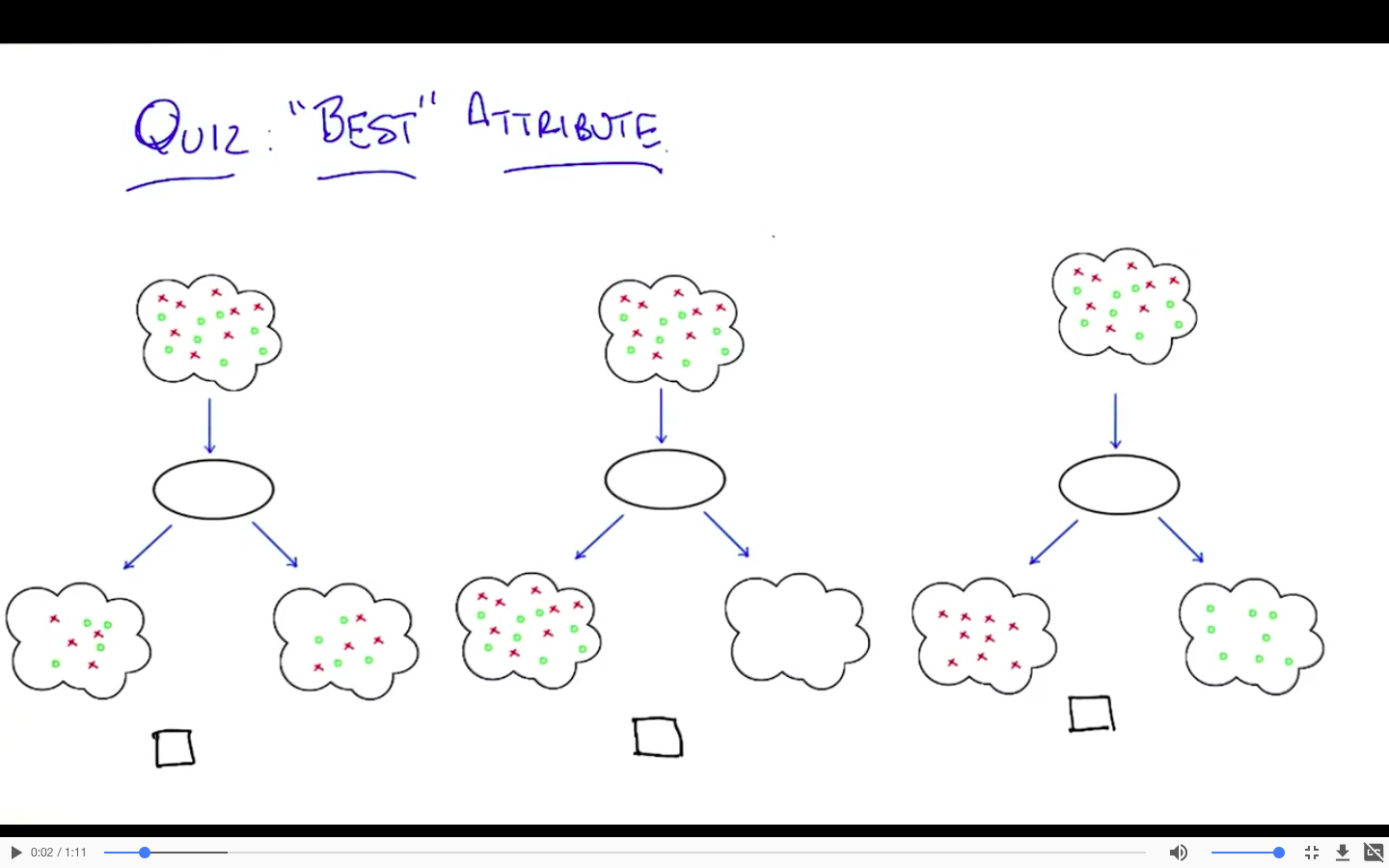
图一图二的entropy没有改变
图三中俩个子集的entropy都减小了,在该例子中,减为0
相应的,它的信息熵的增量是最大的
bias
hypothesis set: all possible decision tree
two kind of biases
- Restriction bias:H
- Preference bias:
- what source of hypothesis from this hypothesis set we prefer

Other considerations

对于存在的噪音该如何处理?
overfitting
- pruning
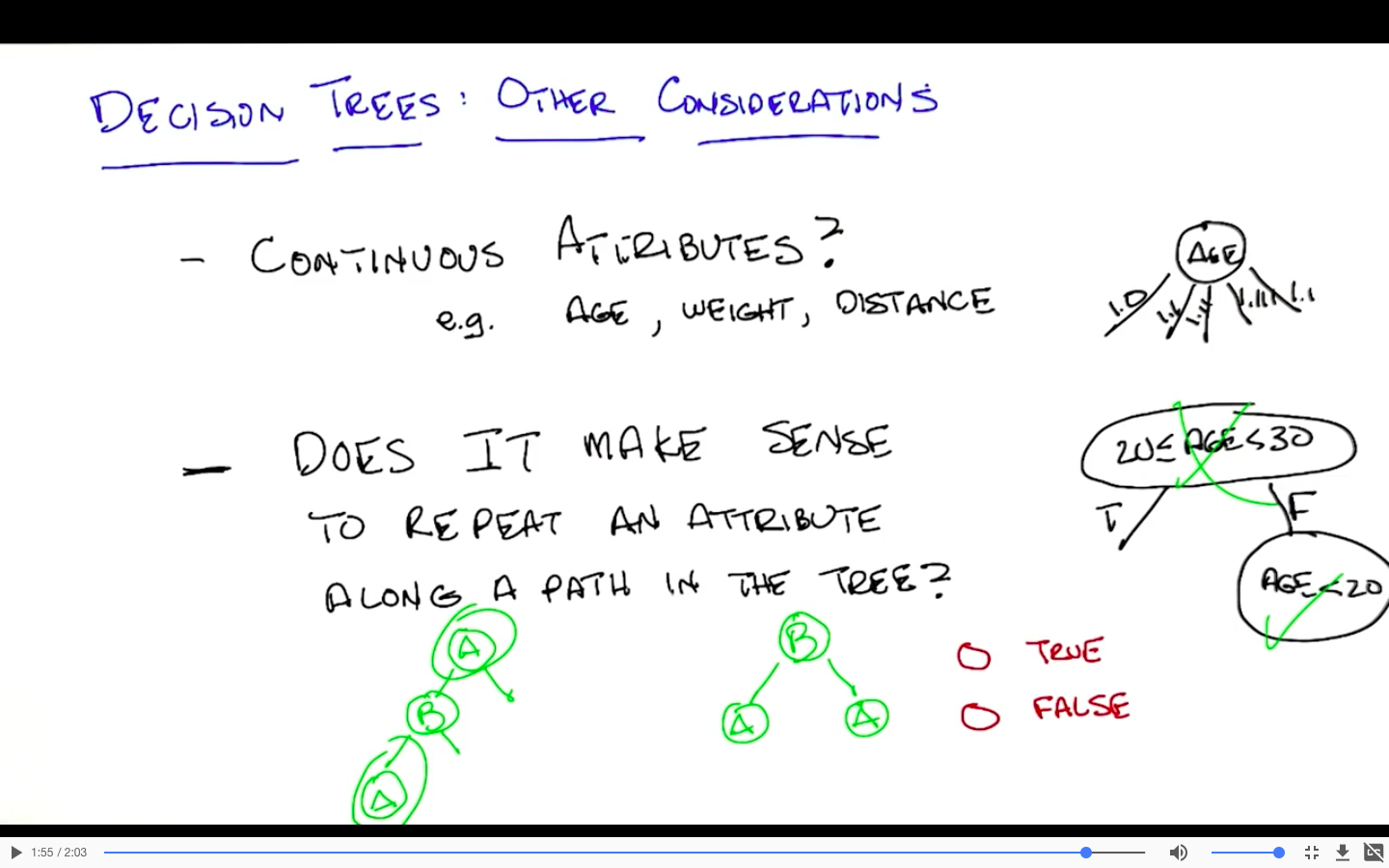
对离散型特征:没有意义
对连续型特征:
- 不同的问题(范围):有意义
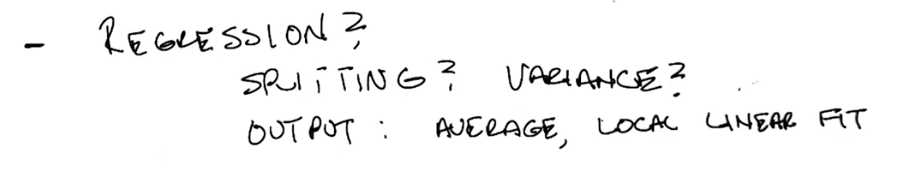
Conclusion
