在阅读李航的《统计学习方法》，周志华的《机器学习》过程中，由于基础不扎实，有些地方理解不了，但是看了补充材料以后，发现对理解有很大帮助，因此在这里想挑选出难理解的点，并进行补充

第5章 决策树

1. P61
   
   
   
   

2. P68
   
   

cost function的形式

cost function的推导满足以下过程：

1. 认为error 满足某个分布，写出样本点xi的样本的error
2. 认为样本点是相互独立的，推导出其对数似然函数
3. 求偏导，是得导函数为0，分离常数部分，得到误差的表达形式

e.g.
线性回归中关于MSE的推导：https://nk2000.github.io/2018/05/16/Linear-Regression/

常见的cost function

均值和中位数的意义

在这样的框架下，假设fx是一个常函数，即fx=c

假设cost function 符合高斯分布时：

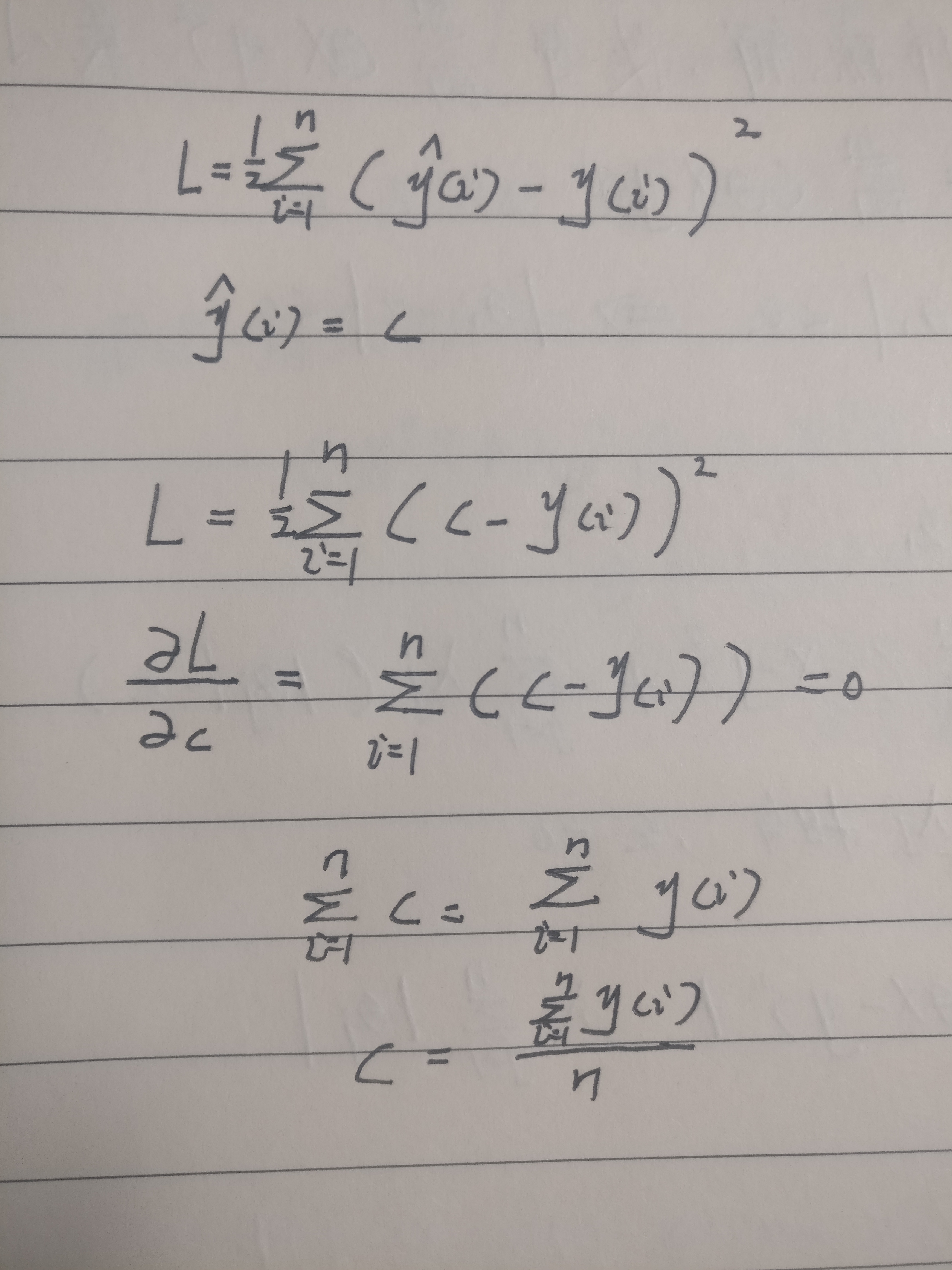
样本的均值就是最好的模型

假设cost function 符合Laplace分布：

中位数就是最好的模型

因此当给定损失函数形式的情况下，一个常函数的模型总是可求的

参考：

1. 邹博博士课件

回顾

1. 决策树的分类能力由叶子节点上的条件概率分布决定
2. 决策树的内路径只决定了特征空间的划分情况，即给定一个样本xi，最终会落在哪个节点

思考：

提升的定义

提升的框架

思路：在构建好的k-1棵决策树的基础上，构建第k棵决策树

符号说明：

这里需要解释一下俩棵决策树的加权和的含义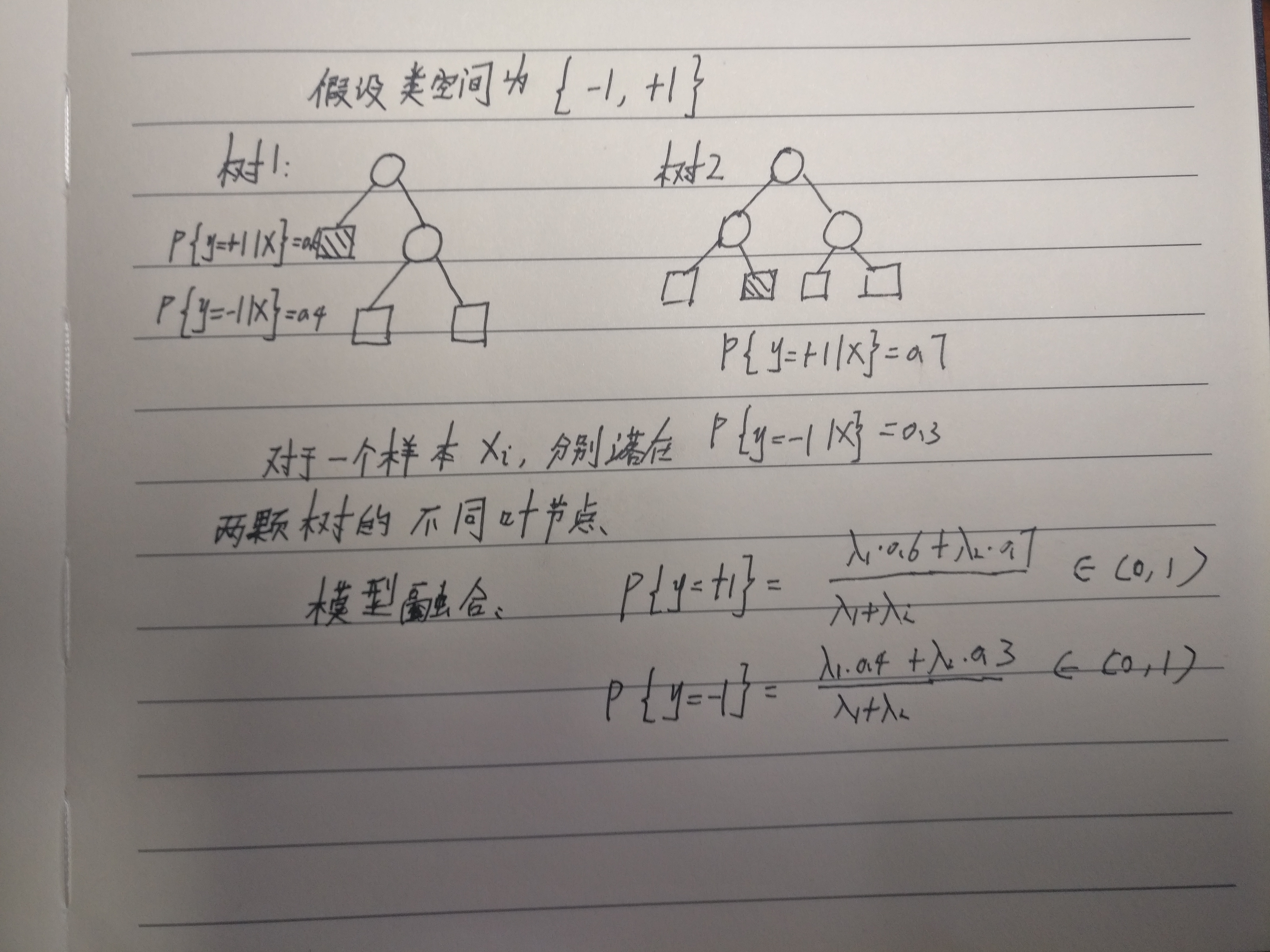

权值a1,a2取值不同，首先决定了不同的特征空间的划分，统计后得到不同的条件概率，是一棵抽象的树结构

1. 首先，给定常函数F0(x):
   
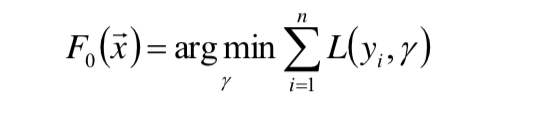
   并且由之前关于cost function中的讨论，F0(X)总是可求的
2. 以贪心的思路扩展得到Fm(x):
   

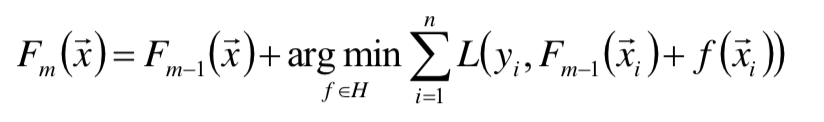
目标函数的计算

这里的所谓权值w就是P(Y|X)的条件分布

模型构建

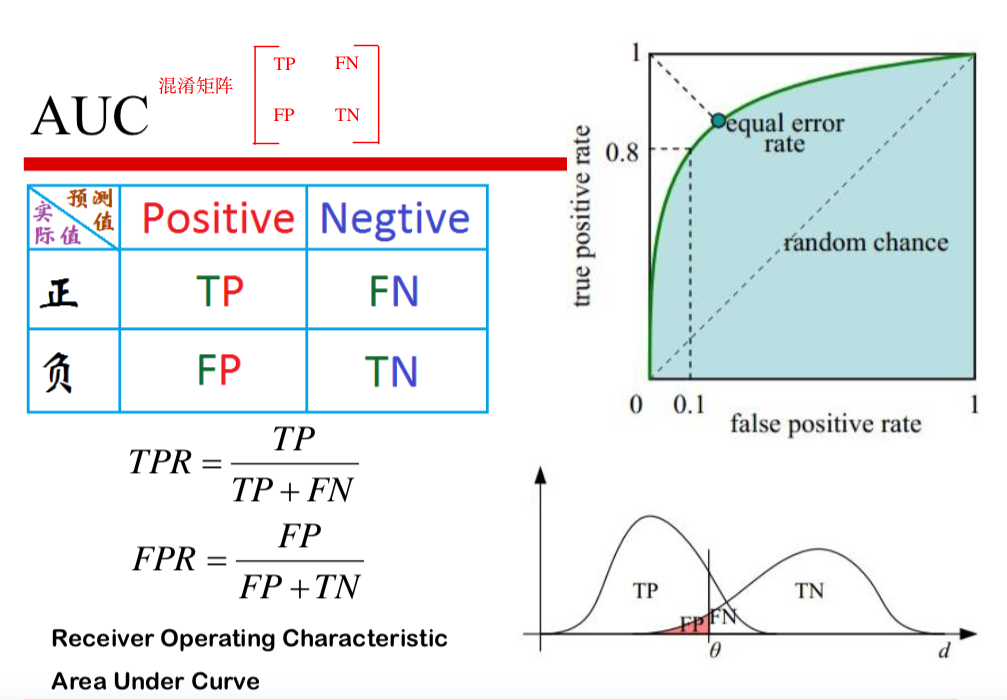
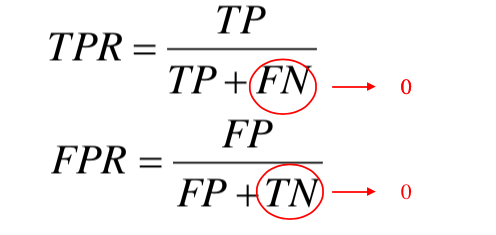
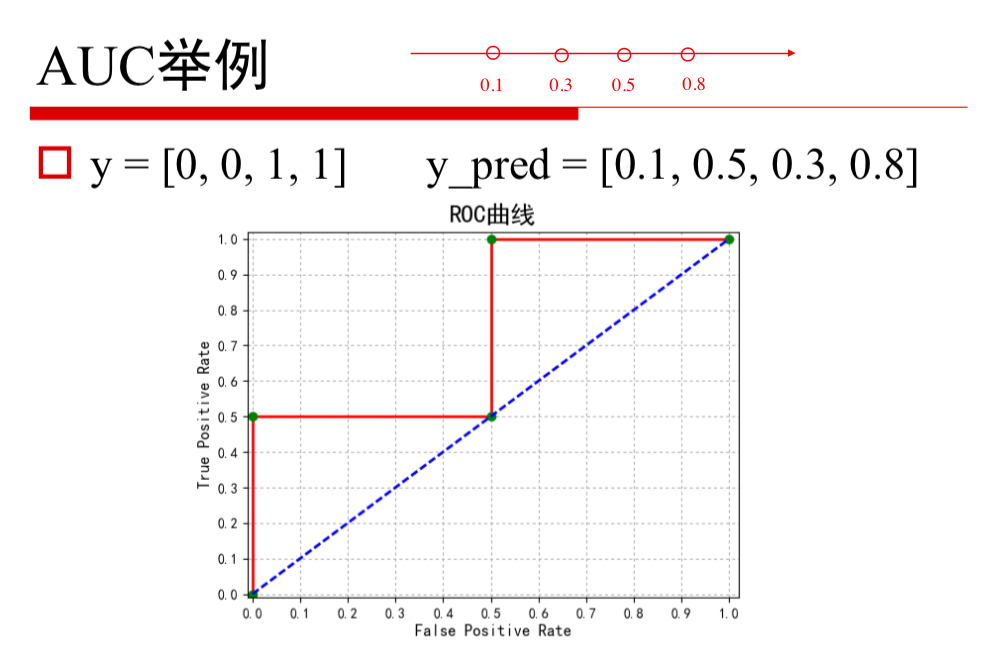
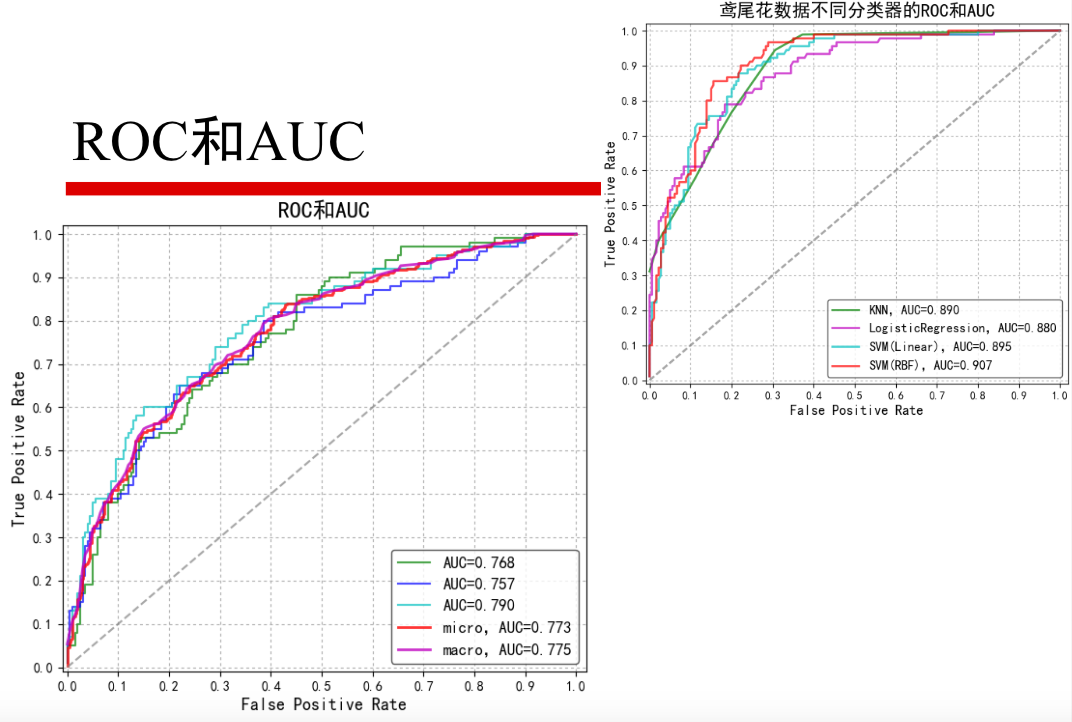
AUC定义

Note:

1. 图像一定过（0，0），（1，1）
   当阈值趋于正无穷时
   
   TPR = 1; FPR = 1
2. 图像一定是上凸的
3. equal error rate曲线所围成的面积越大，代表着模型越好
   当预测越准确时，TPR，FPR都接近1，故面积大

AUC实例

阈值的取值不同，AUC的图像也不同，在此例中，0.1，0.3，0.5，0.8把数轴划分成了5个区域，每个区域中的AUC取值是相同的，不同的区域，AUC取值不同，分别对应着图中的五个点

之前的图是对应着4个样本点的情况，故有很明显的折线，当样本点个数增多时，AUC的效果会趋于上图

Note：
感觉还是没懂，待续…

参考

1. 邹博博士课件
2. http://alexkong.net/2013/06/introduction-to-auc-and-roc/

模型表示

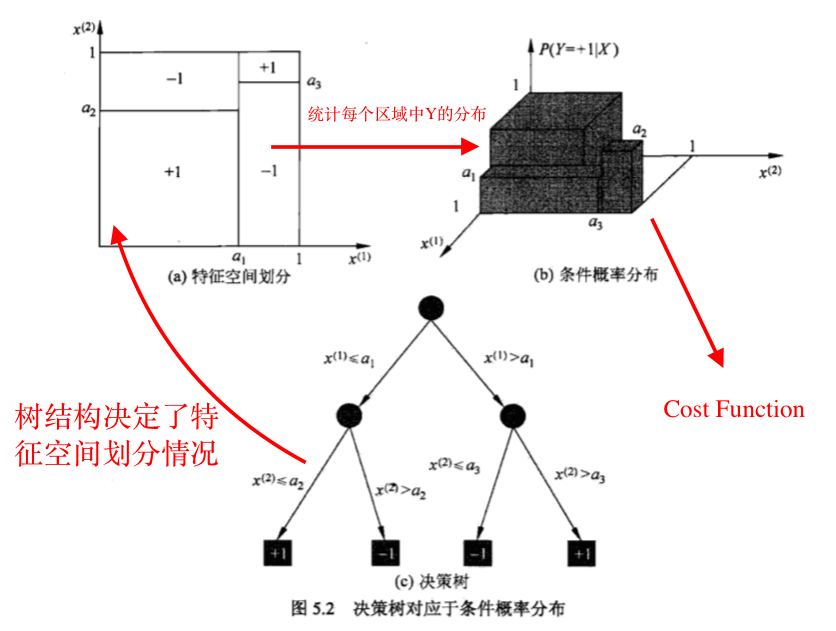
决策树算法的本质是求出最优的特征空间的划分，在这个划分基础上的条件概率P(Y|X)的分布最优

因此还需完成俩步：

1. 定义 cost function
2. 根据cost function怎么构建决策树（因为决策树的结构决定了cost function）

代价函数

从模型表示可以直观地看出，叶子节点中Y的种类越少越好，意味着分错的数量越少

叶子的熵可以量化这一情况

决策树的构建

因此决策树学习的算法转变为了递归选择最优特征的一个过程

接下来给出如何选择，定义最优特征

特征的选择

根据不同的最优特征定义，分别有着不同的决策树学习算法

信息增益

1. 确定度量量
   学习算法的目标就是降低整棵树的信息熵，因此认为最优的特征A是，在确定A后，特征空间D的信息熵减少最多的那个特征
   

2. 条件熵的公式推导
   由此可知，条件熵恰好可以用来帮助选择特征，下面给出条件熵的公式推导，便于计算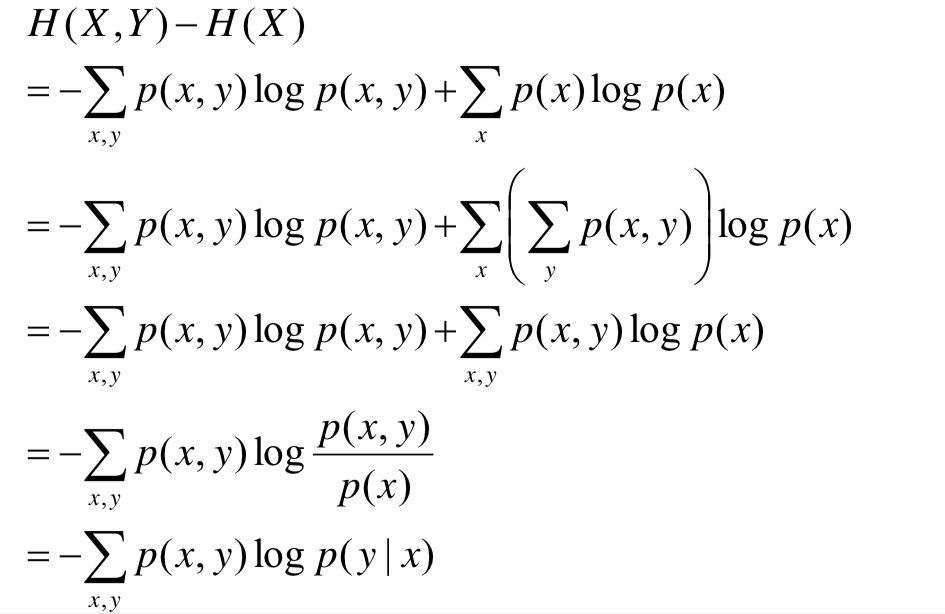
   
   

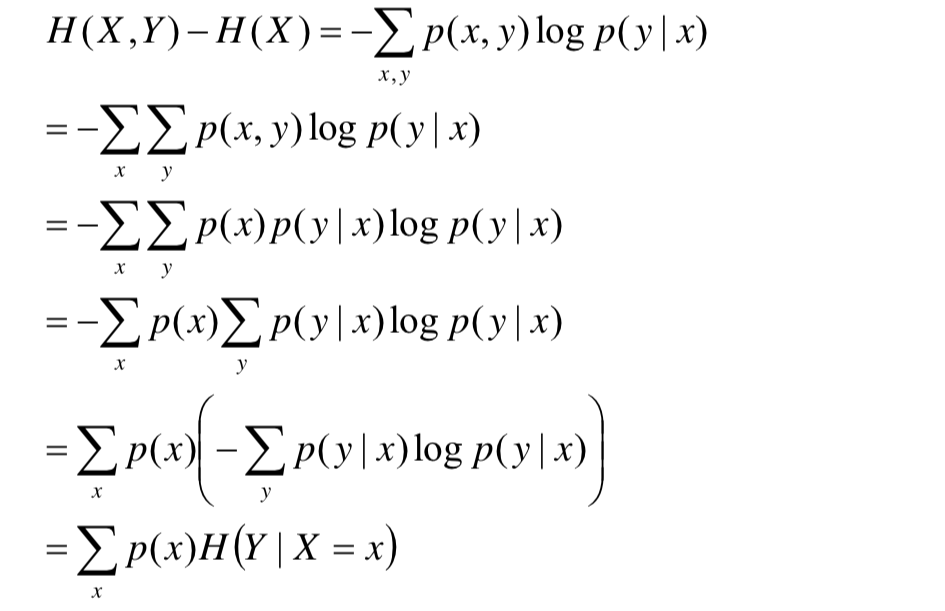
3. 信息增益的定义
   

4. 信息增益的计算
   符号定义
   
   公式计算
   

信息增益比

参考：

1. 邹博博士课件
2. 《统计学习方法》——李航

模型定义

特征 x：m*n
label y：m*1
不同的x，@对应一个不同的二项分布
这些二项分布可以通过统计求得

改进

不按照x是否相同，来统计其二项分布的分布律，而每一个样本点都看做一个独立二项分布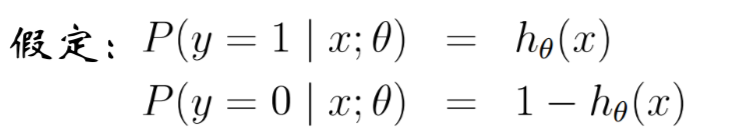

这样的特点就是这样的二项分布只有俩种，分别为

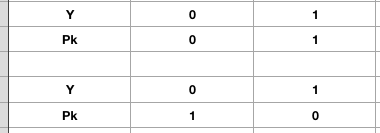
并且能合并表示为

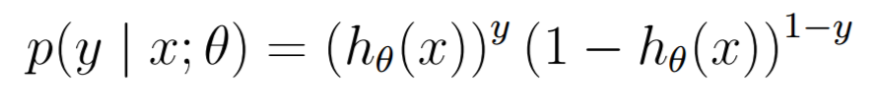
目标函数——交叉熵

小目标：对于每一个样本点，分别求出一个分布，使得俩者分布差距最小

模型目标：所有的样本差距之和最小

KL散度

Kullback-Leibler Divergence，即K-L散度，是一种量化两种概率分布P和Q之间差异的方式，又叫相对熵。在概率学和统计学上，我们经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息。
参考链接：https://www.jianshu.com/p/43318a3dc715

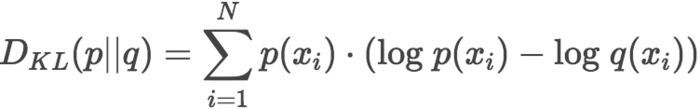
K-L散度是数据的原始分布p和近似分布q之间的对数差值的期望

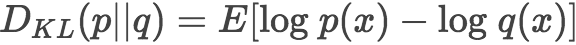
其中分布p是我们上面统计出来的数据分布

KL散度与交叉熵的关系

目标表示

小目标：对于每一个样本点，分别求出一个分布，使得俩者分布差距最小

模型目标：所有的样本差距之和最小

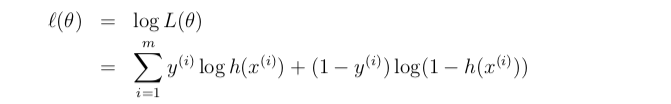
目标函数——极大似然估计

同样认为对于每一个样本点都是一个P(y)的二项分布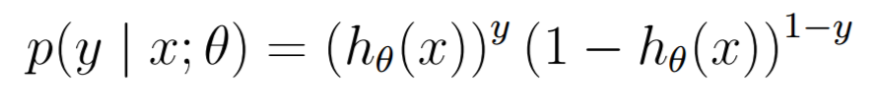

L() 代表获得到样本的概率，希望概率越大越好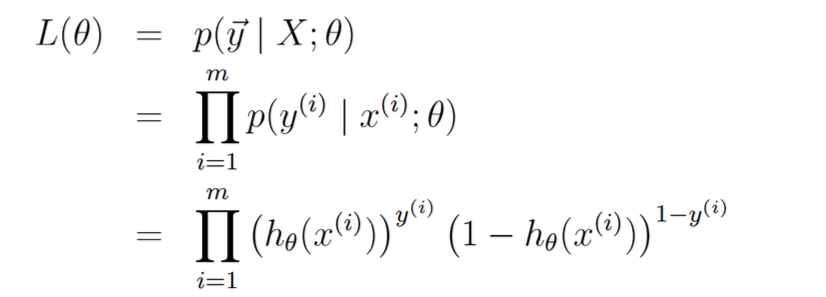

求对数似然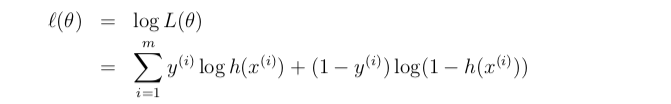

模型求解

参考:

1. KL散度的介绍：https://www.jianshu.com/p/43318a3dc715
2. KL散度，交叉熵的关系；在Logistic回归中的应用
3. 邹博老师的课件

Loss Function

• 理论基础：中心极限定理
  • 误差符合高斯分布

• 公式推导
  
  

解释了为什么损失函数是这个形式

模型求解

意义：理论上推导出模型可解，但对矩阵求导，计算量很大，实际不采用

对目标函数求梯度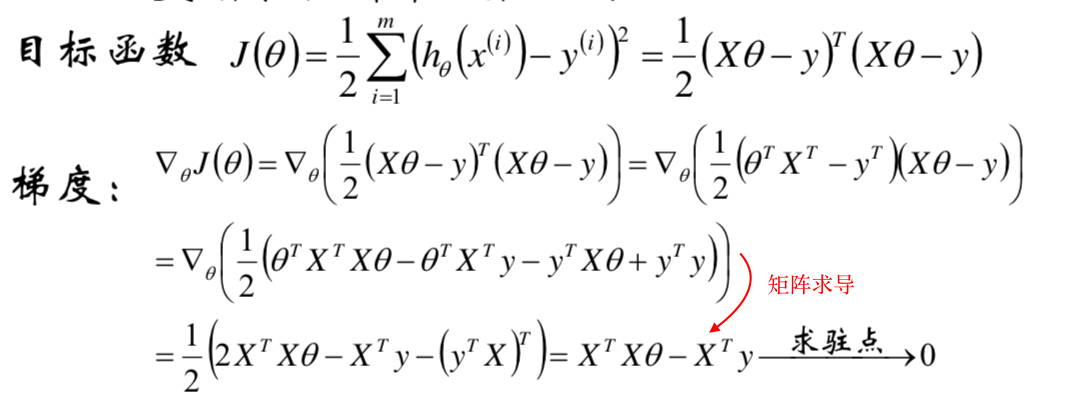

使梯度为0

为什么能添加扰动能防过拟合？

通过实践可得，当n维特征向量映射成更高维的特征时，最后求解得到的参数值都很大，因此希望在原loss function基础上添加关于参数的项，来作为对模型复杂度的惩罚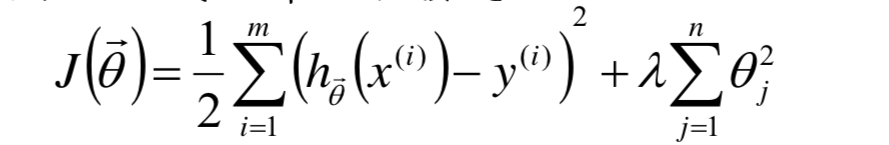

为什么加了扰动后一定可逆？

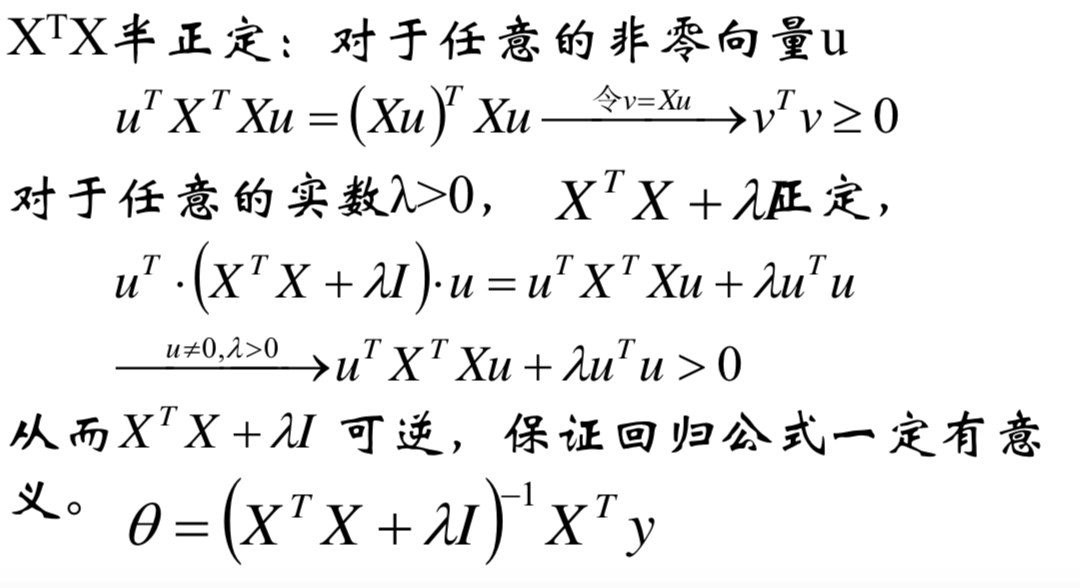
对新的目标函数求梯度

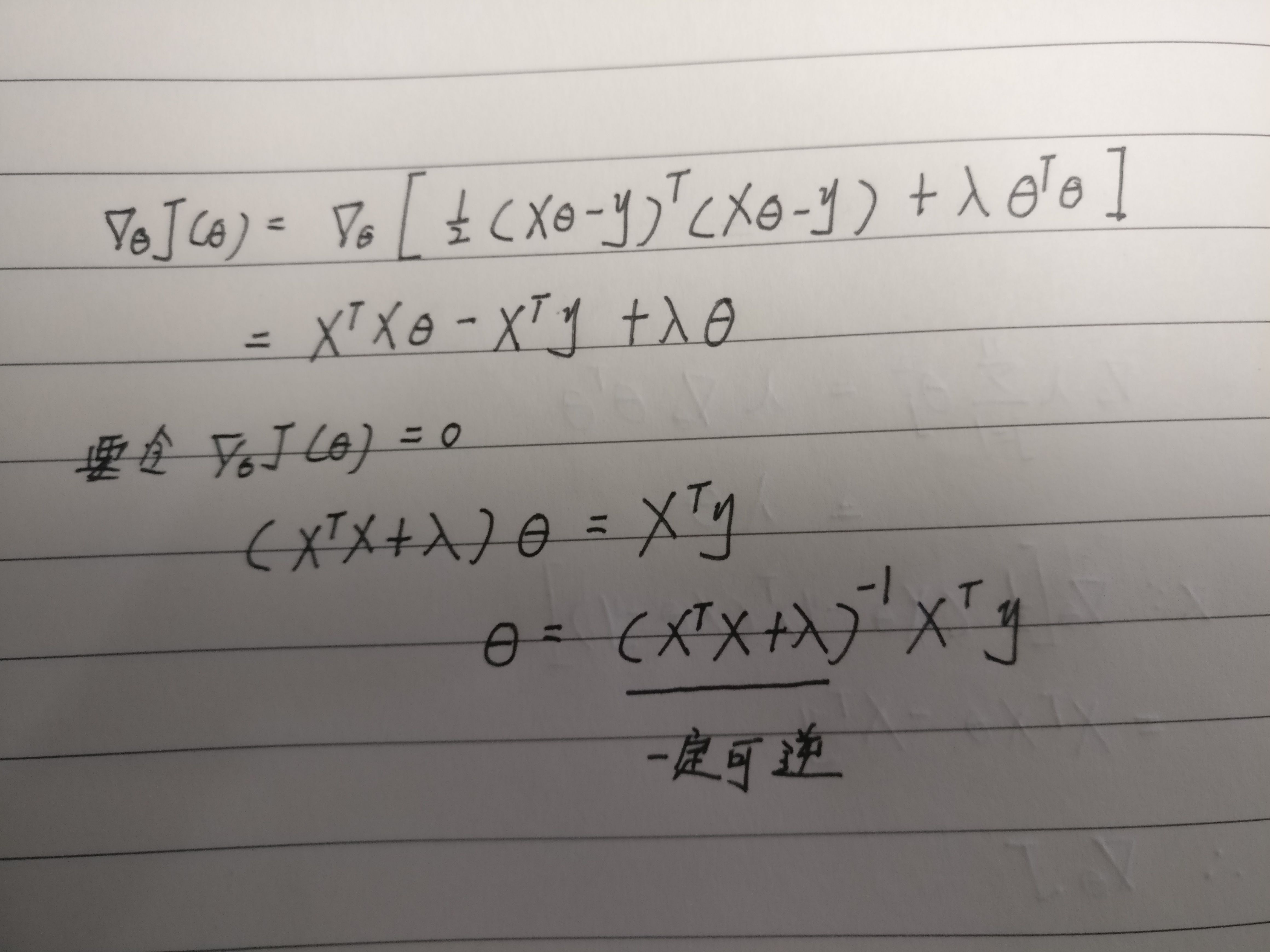
复杂度惩罚因子

LASSO：

• L2-norm：性能往往不错，但没有特征选择功能
• L1-norm：高阶系数接近于0，相当于进行了特征选择
• Elastic Net：L1-norm与L2-norm融合

感性解释：从实验出发，跑代码，当过拟合发生时，其系数很大，因此想把其系数也作为损失函数的一部分

帮助理解的解释：
拉格朗日乘子法，推导出L1-norm的形式

广义逆矩阵（伪逆）

模型优化

• 批量梯度下降算法
  
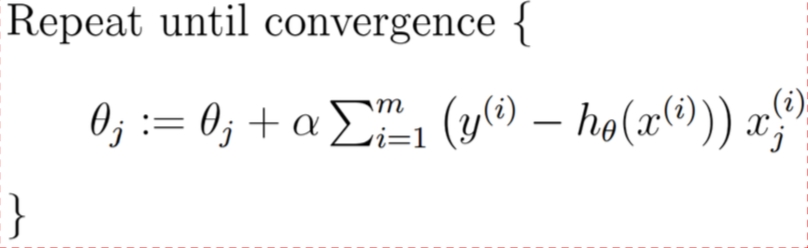
• 随机梯度下降算法：支持在线学习
  
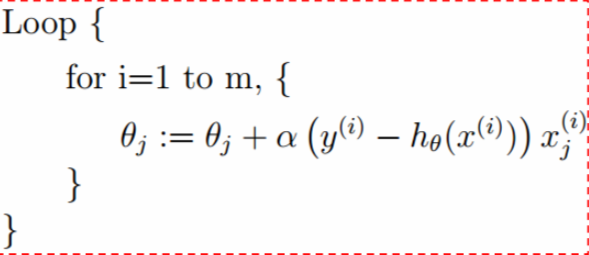
• mini-batch

优化问题

• 无约束优化问题
  • 梯度下降法
• 有等式约束的优化问题
  • 拉格朗日乘子法
• 有等式约束的优化问题
  • 拉格朗日对偶性

问题分类

• 线性可分支持向量机
• 线性支持向量机
• 非线性支持向量机

线性可分支持向量机

原理和目标：What

目标

求一超平面，样本点到超平面的距离尽量地大——较好的泛化能力

表示

1. 问题转化
   求出离超平面最近的样本点的距离，并使得该距离尽量地大
2. 样本点到超平面的距离
   • 公式1
   • 去除公式中的绝对值
3. 考虑到实际做的过程中可能会将特征映射到更高维
   引入特征空间转换函数
   • 目的，待会儿帮助解释核函数
4. 函数间隔&几何间隔
5. 原始形式不好求解，寻找等价命题
   简化为目标函数 + 条件约束

模型求解：How

步骤

1. 写成拉格朗日乘子法的形式
2. 因为其满足KKT条件，利用对偶性
   min max 问题转化为 max min 问题
3. 求min
   求偏导，回代，求max{new function}
4. 求解

例子

结论：

1. a不为0的样本点为支撑样本点
2. a为0的样本点对模型构建没有影响

线性支持向量机

引出背景

1. 样本线性可分，但在全分对情况下，模型可能不是最好的
   • margin小
2. 样本线性不可分

模型表示

添加松弛因子

c的含义——对错误的容忍程度

• 影响泛化能力
• 影响margin宽度

模型求解

损失函数分析

1. 损失函数图像
   横坐标是样本点到支撑超平面的距离
   纵坐标是损失值
2. 基于图像，得到新的loss function，引出hinge损失
3. 解释前面求解出的损失函数的意义